Most trig applications deal with degrees – in fact, our brains naturally tend to think in terms of degrees too. Haven’t you heard the phrase, “he turned a 180” or “make a 360”?
Degrees just comes naturally to us.
So why change?
Well, the problem with only working with degree measure is that it limits our ability to apply angles to other functions because we’re stuck with values between 0 and 360.
In fact, as Purple Math explains, a degree is not a number we can do most mathematical computations with. It’s very similar to the idea between a percent and a decimal.
If I said, we have used up 50% of our storage space, we all have a clear picture. But, if we wanted to do any mathematical computation then we have to convert it to a useful number, which means we have to convert it to its decimal form of 0.5.
So how do we fix the problem?
Huh?
Picture a circle.
Now we know two things:
I still don’t get it.
Here’s another way to look at it…
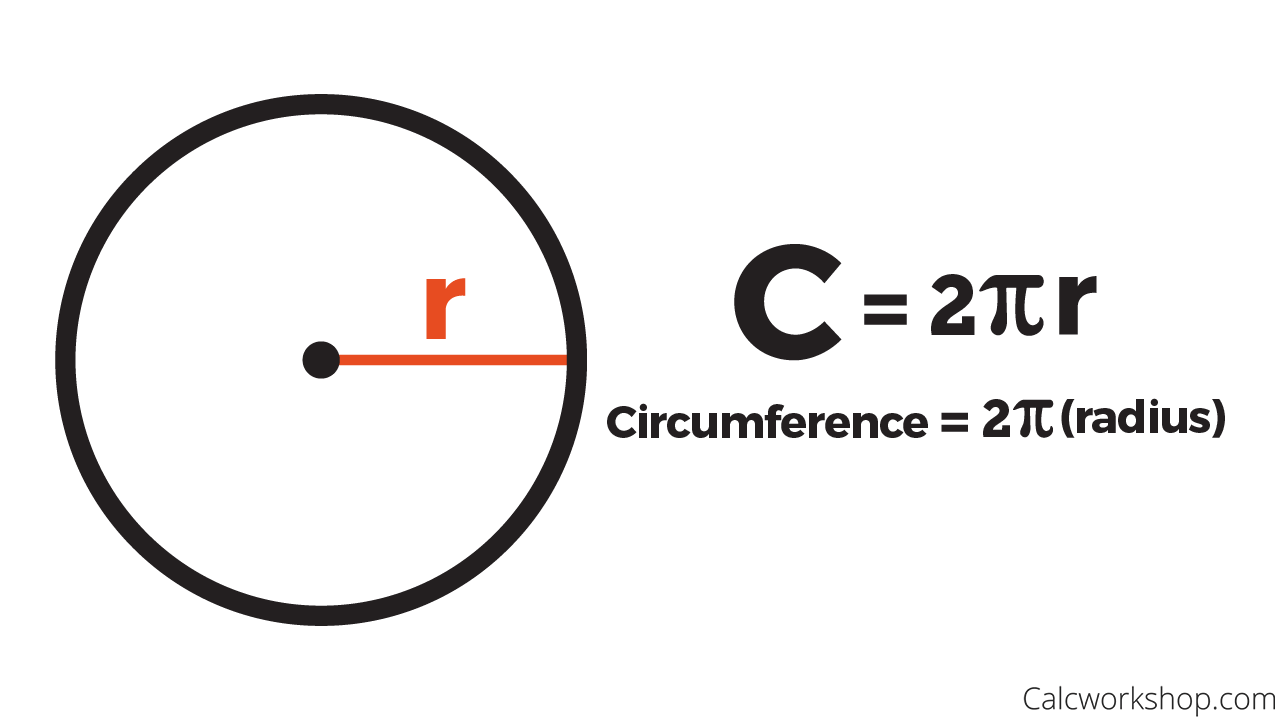
Remember when we created our unit circle? Well, we specified that our radius was the value of 1, right? So, if we then want to calculate our circumference of this unit circle, our distance around would be 2pi.
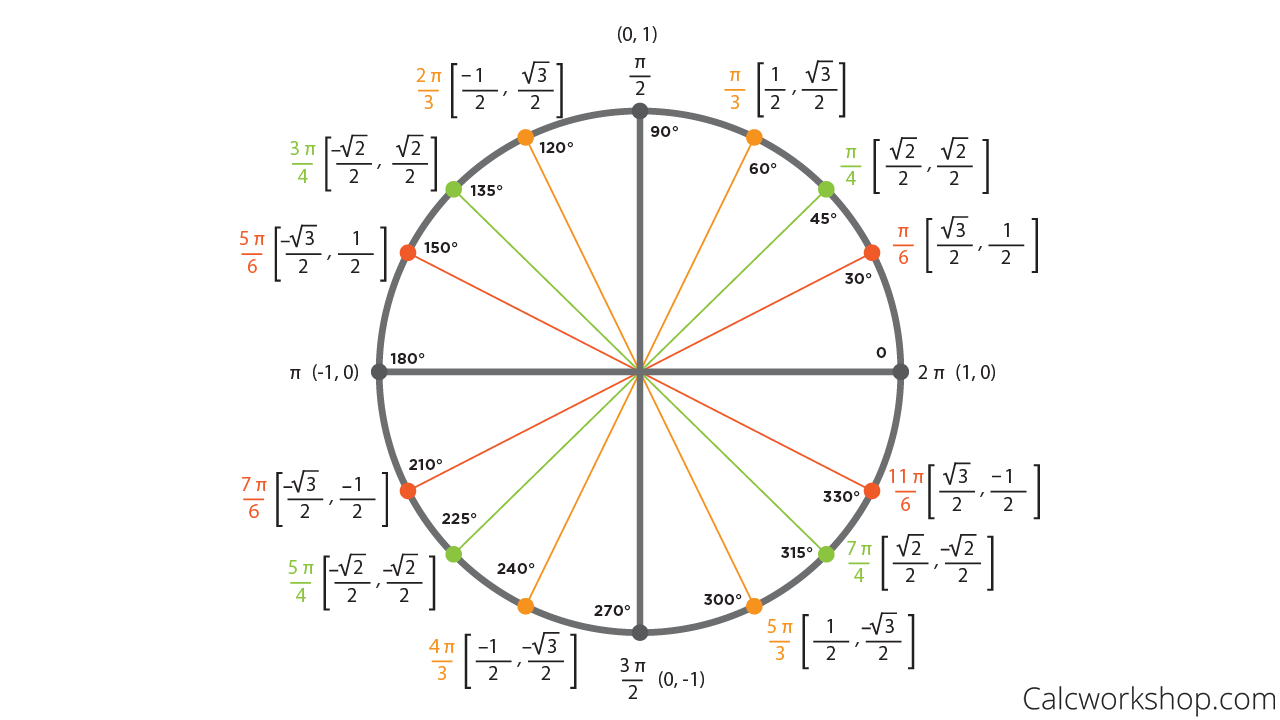
Ah, now I see. So in our unit circle, we have a circumference of 2pi, which means I’ve gone all the way around which is just like rotating 360 degrees as seen in the unit circle diagram below.
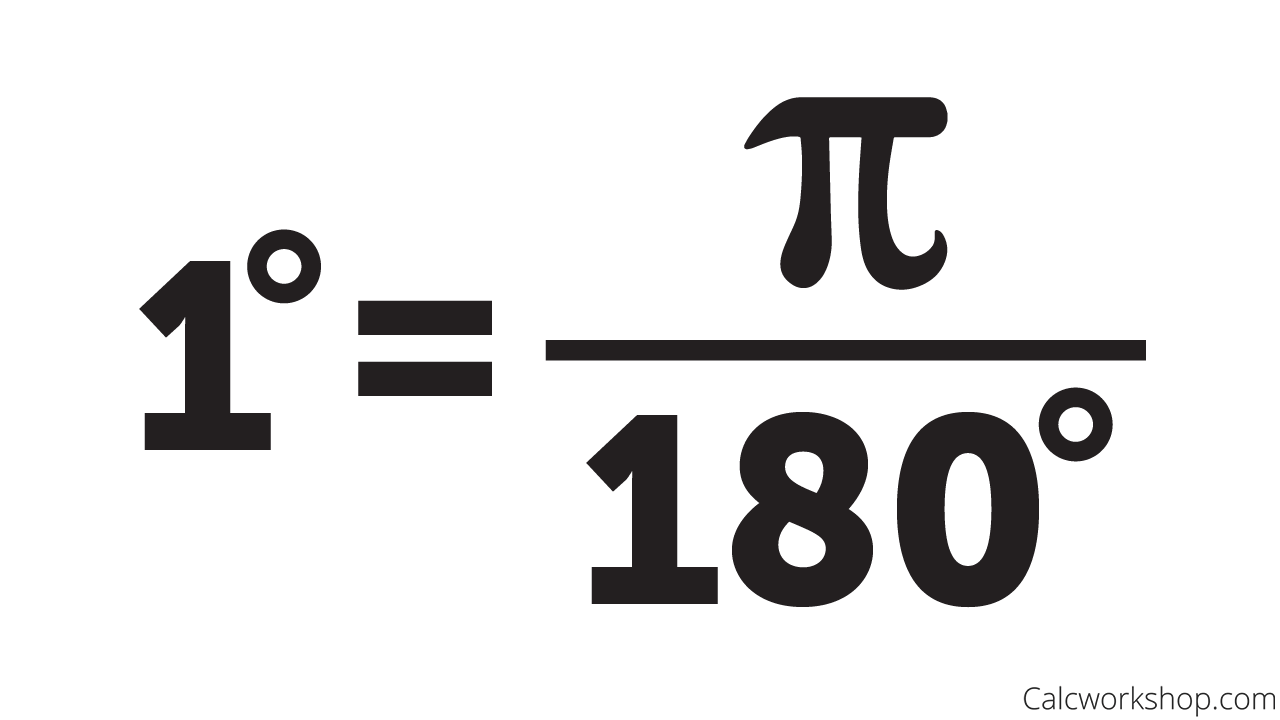
But why do we even have to do this? This seems like a lot of work, and I’m already happy with degrees – they’re easy and comfortable.
In more advanced mathematics, the use of radian measure is preferred and often required to solve problems. To deal limits and derivatives, which helps us to explain how things change over time, we have to use radians – and over time, you will see that radians are easy, fun, and very, very helpful!
Trust me…
…radians are friends!
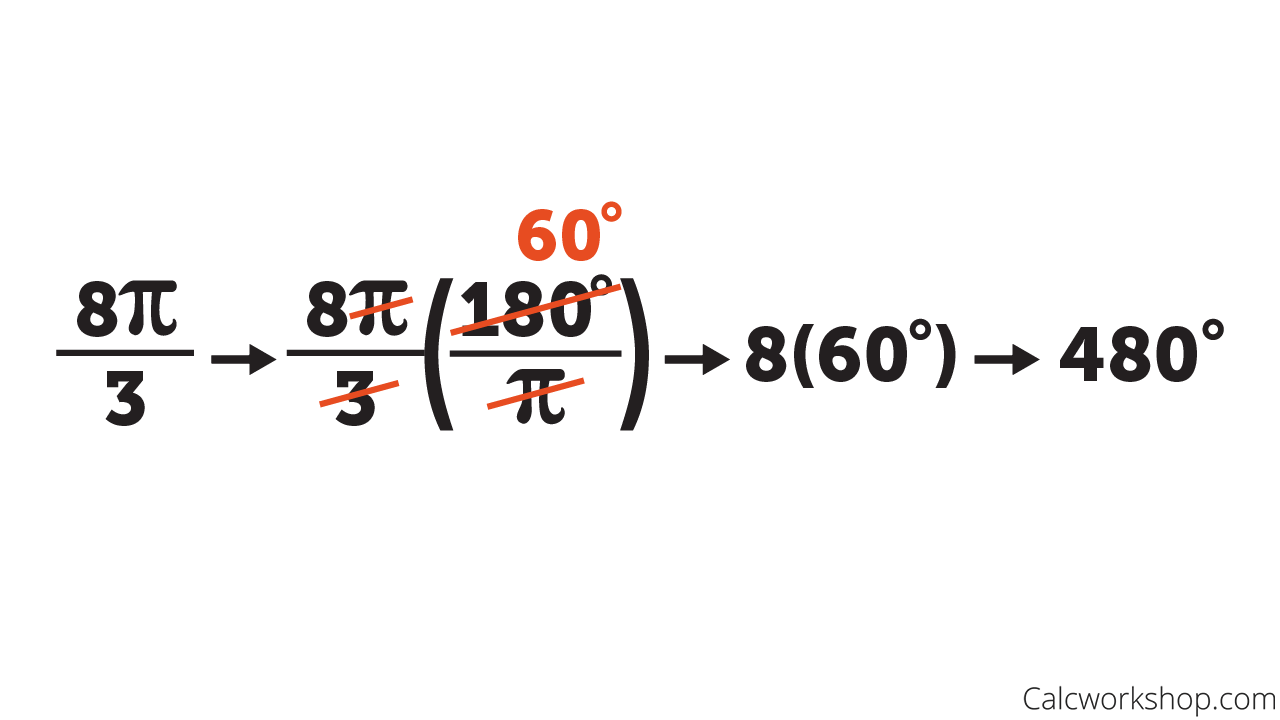
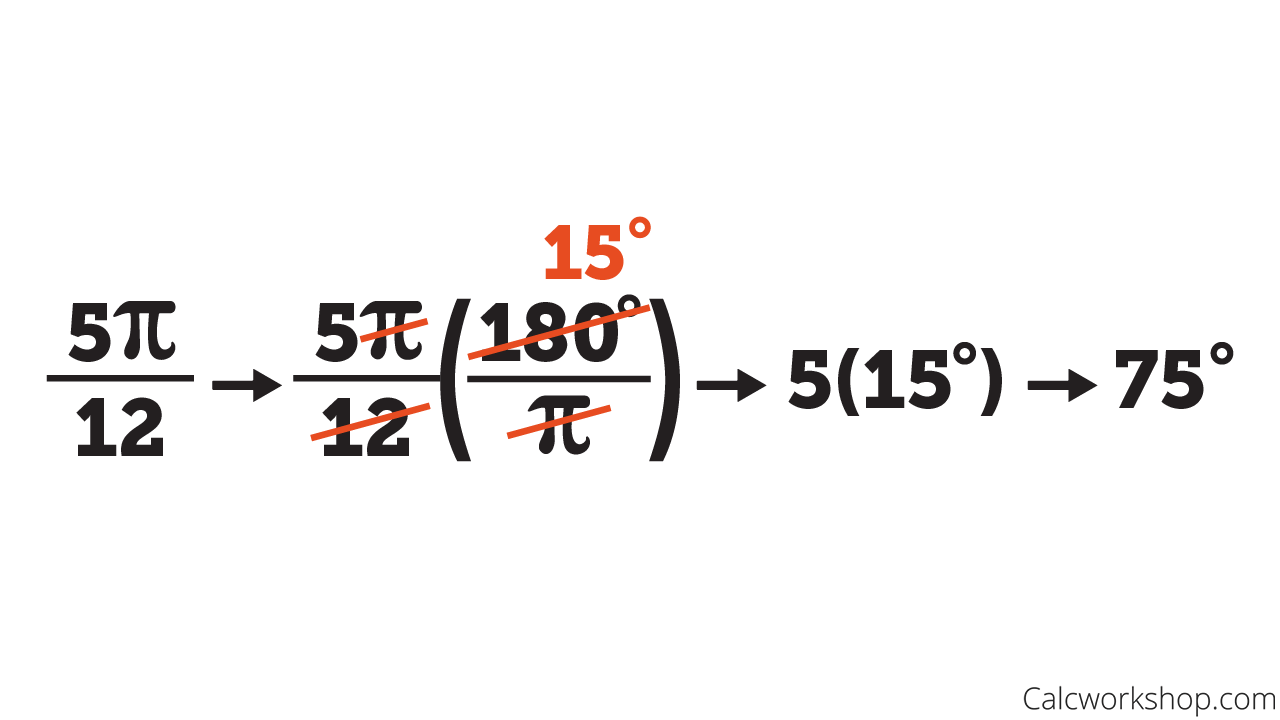
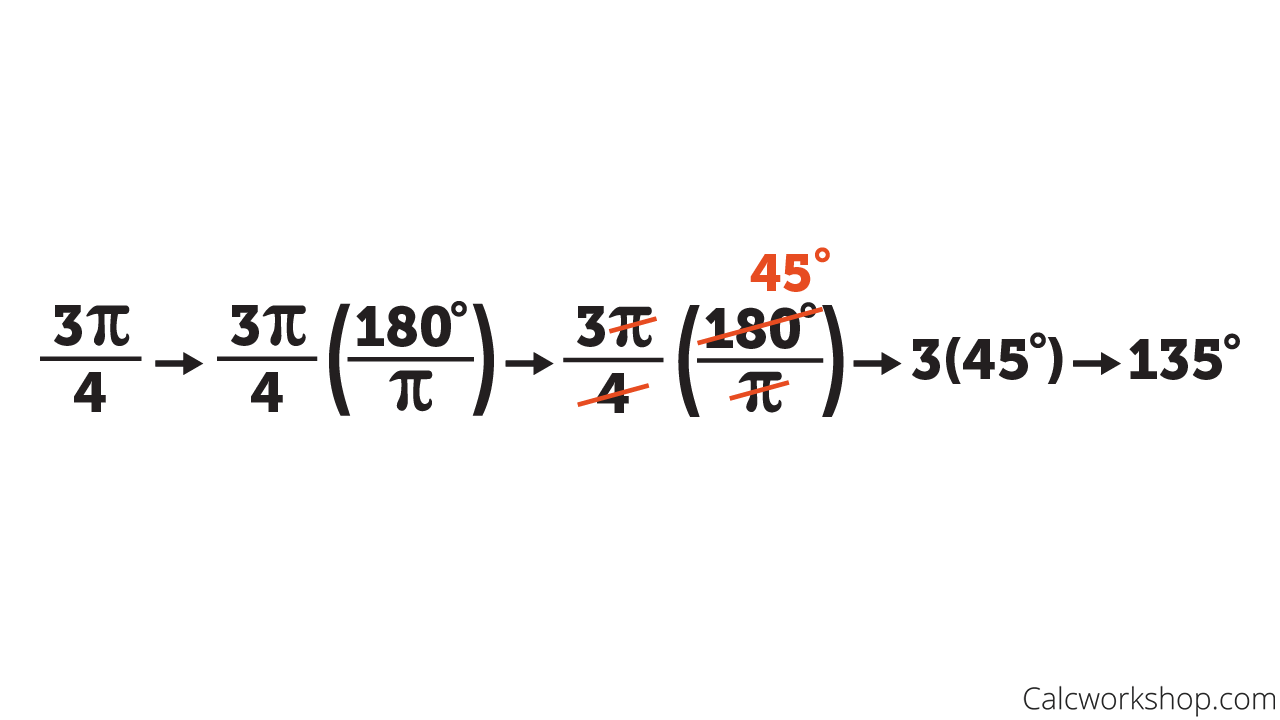
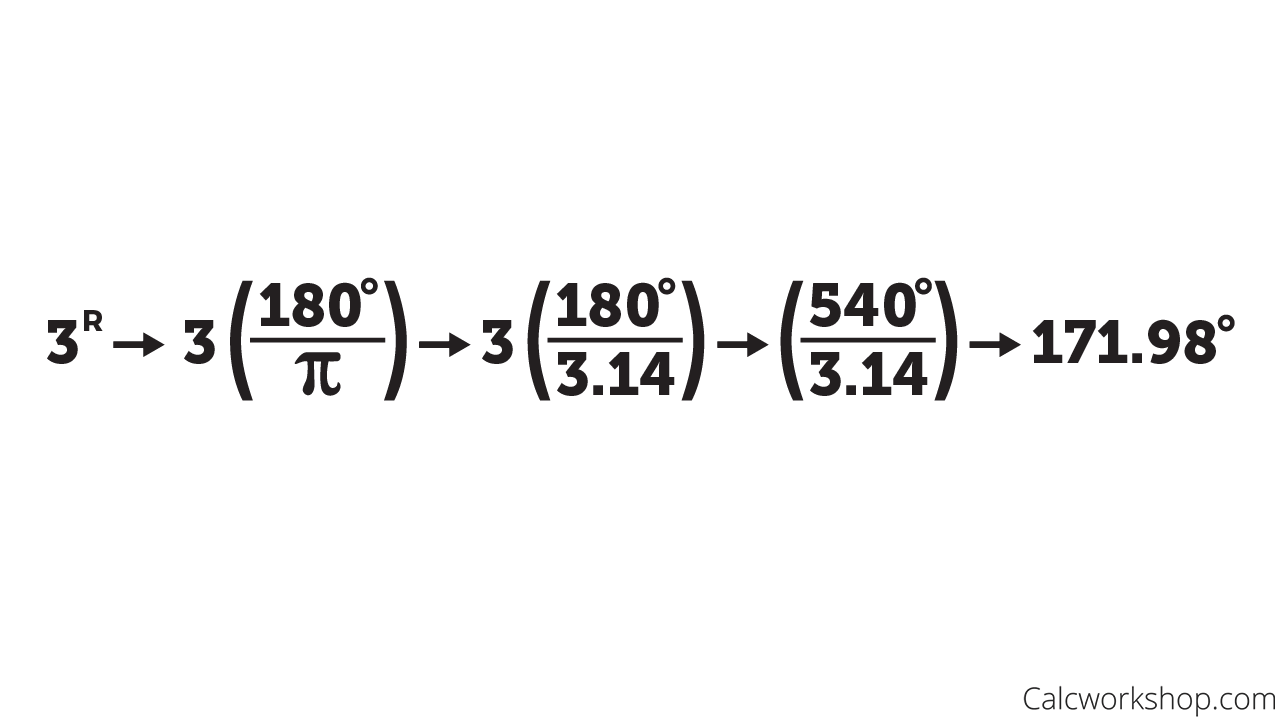
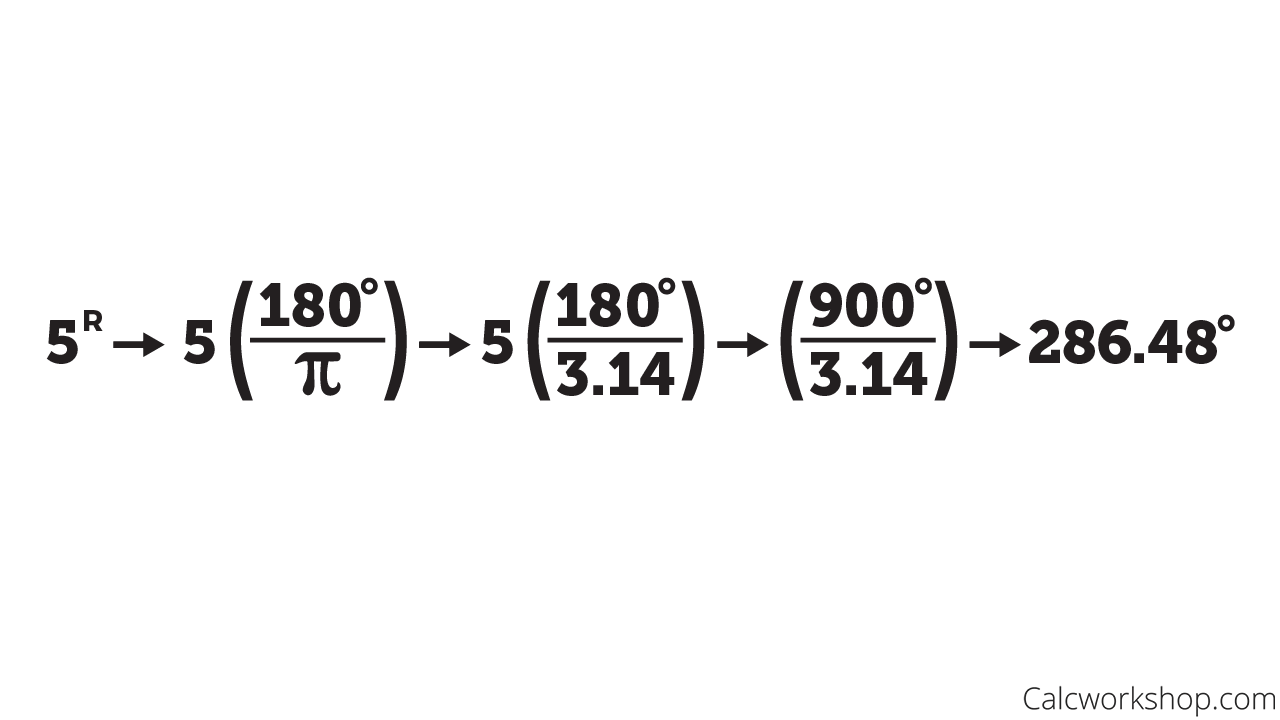
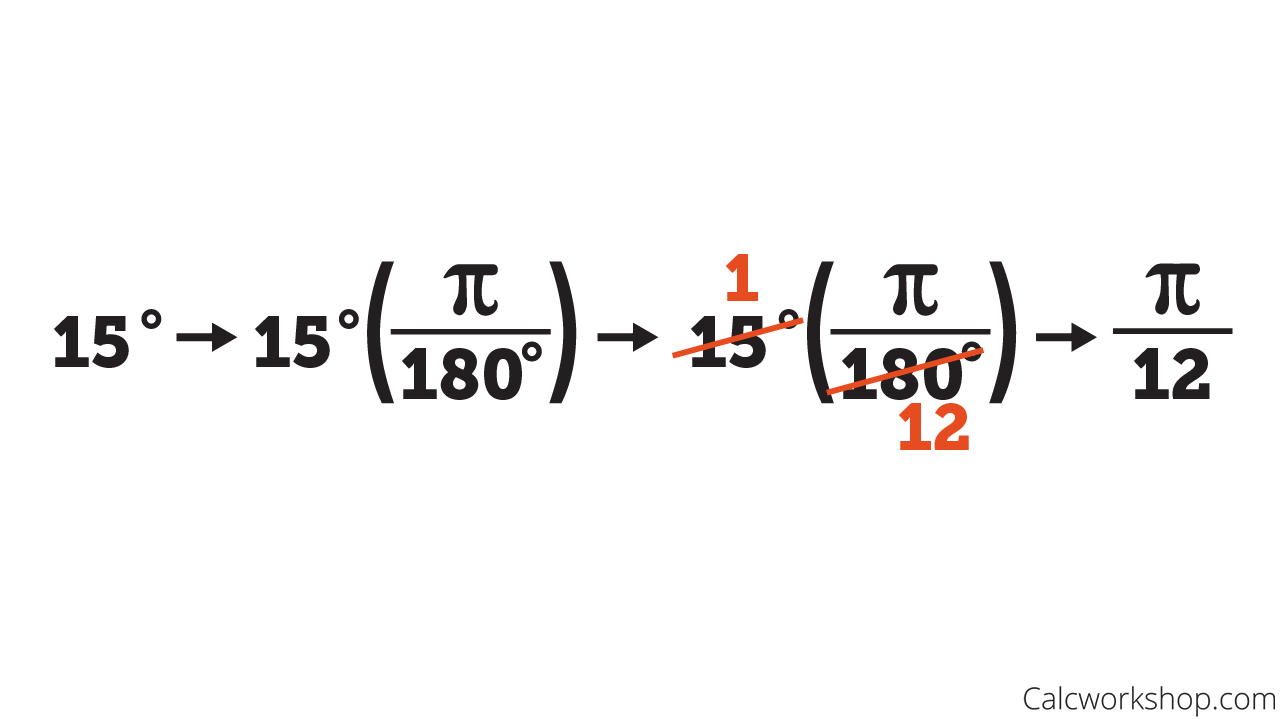

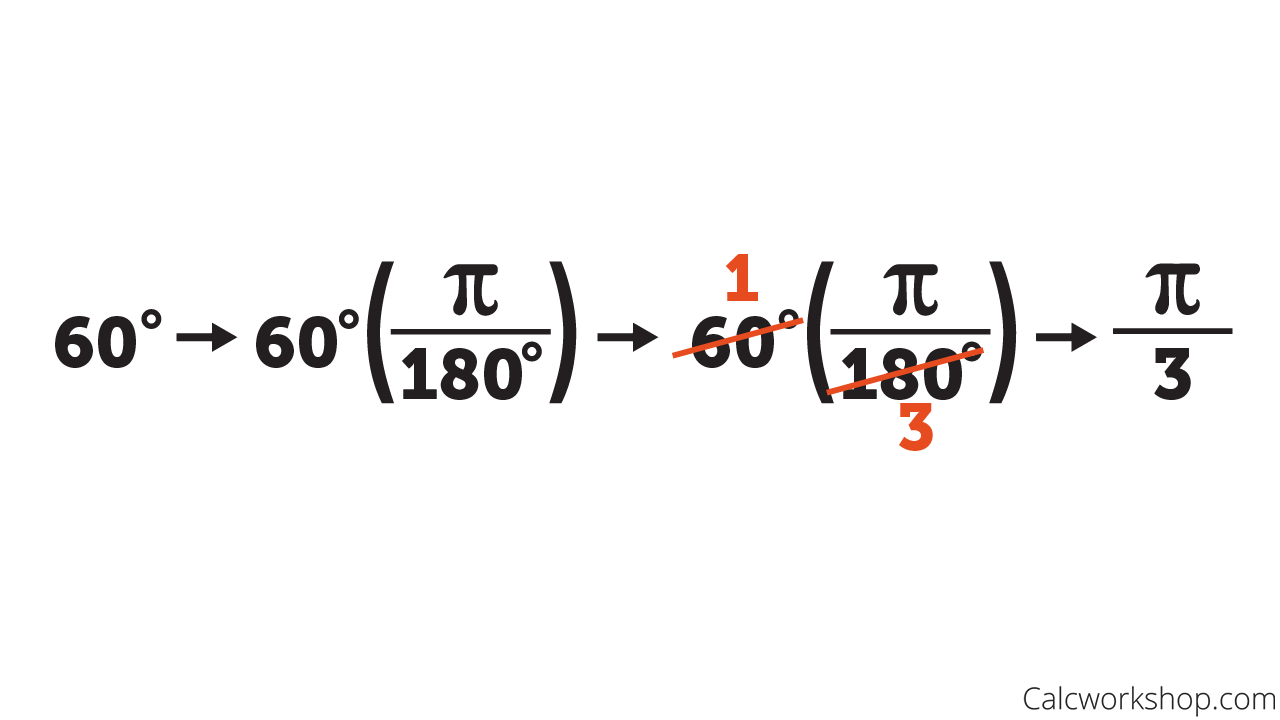
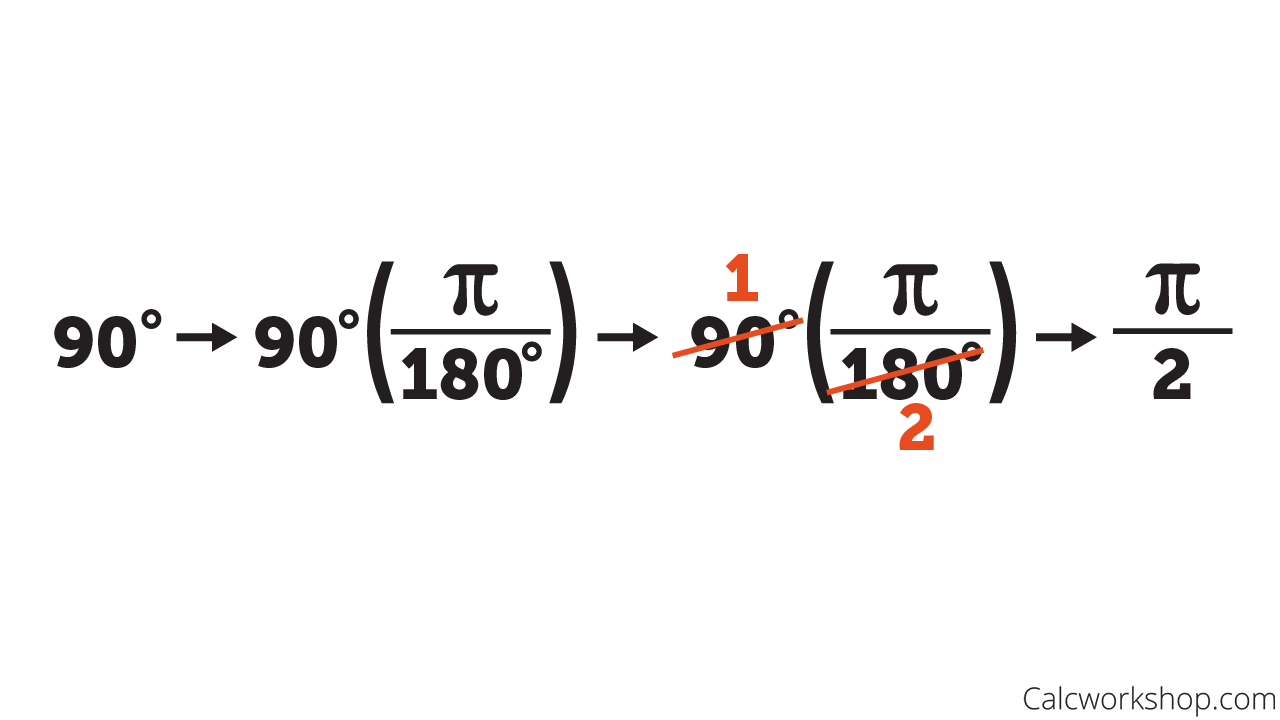
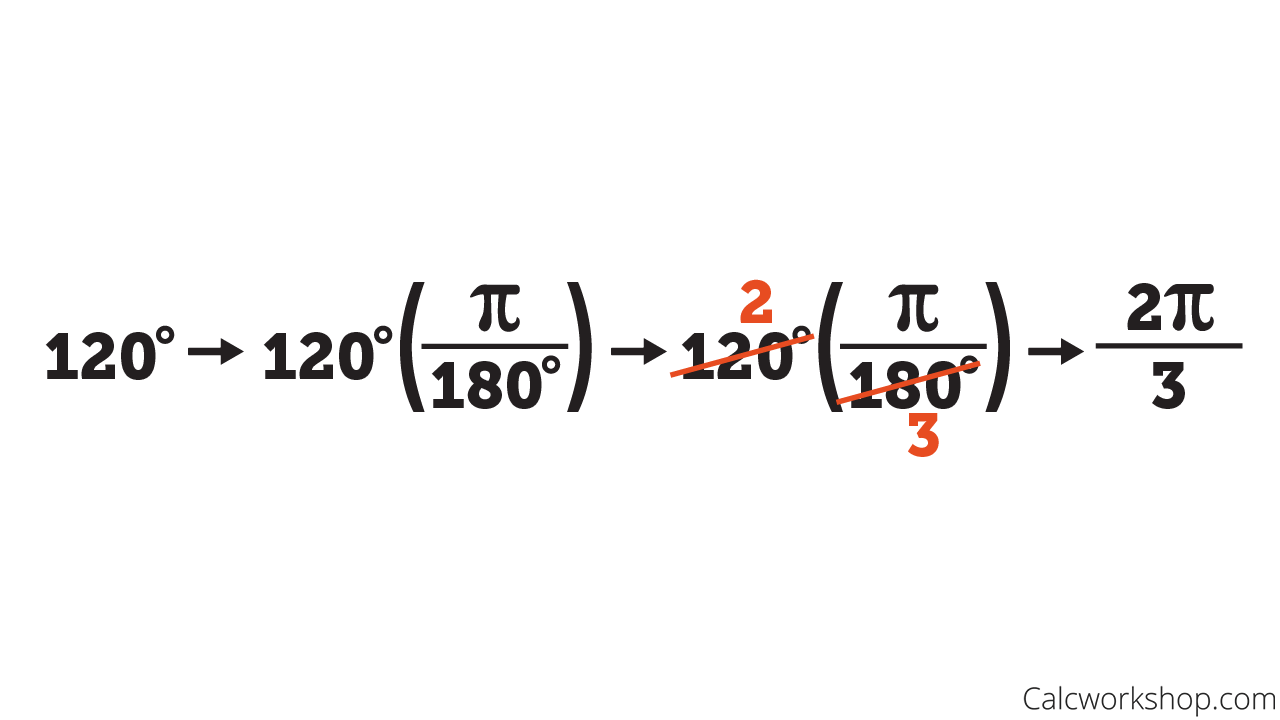
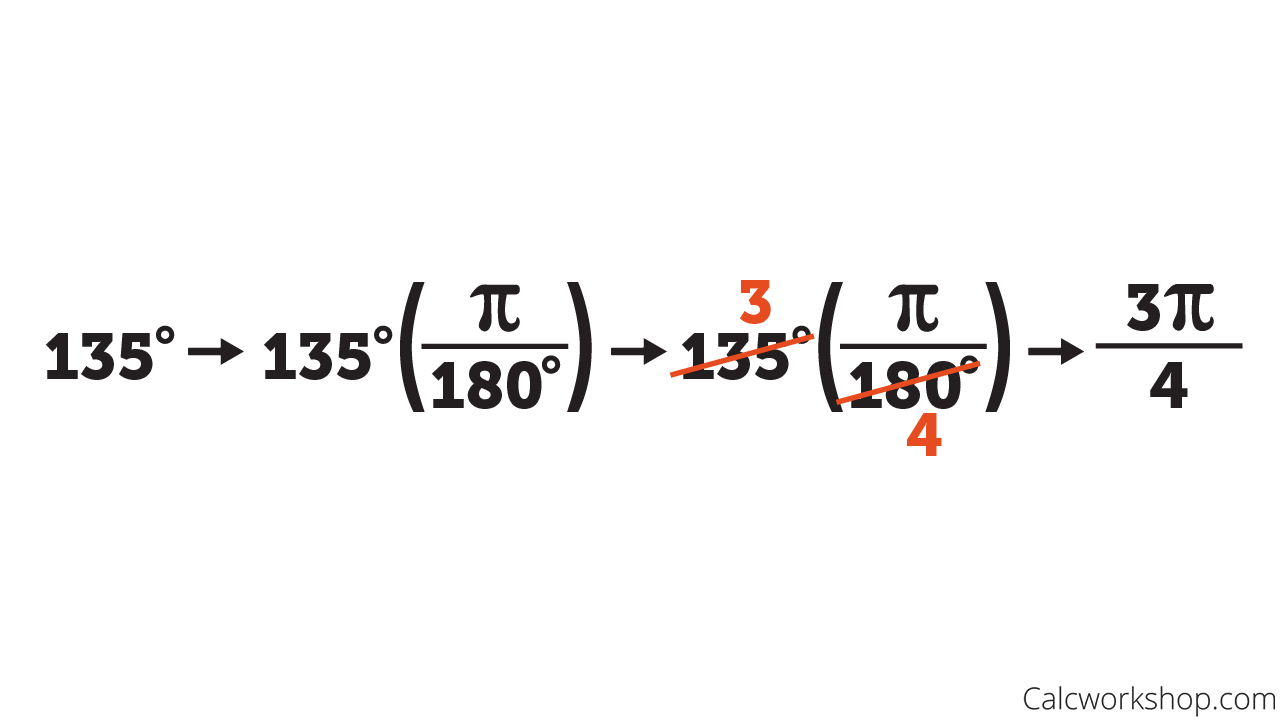
Get access to all the courses and over 150 HD videos with your subscription
Monthly, Half-Yearly, and Yearly Plans Available
Get My Subscription Now
Not yet ready to subscribe? Take Calcworkshop for a spin with our FREE limits course

Degrees just comes naturally to us.
So why change?
Well, the problem with only working with degree measure is that it limits our ability to apply angles to other functions because we’re stuck with values between 0 and 360.
In fact, as Purple Math explains, a degree is not a number we can do most mathematical computations with. It’s very similar to the idea between a percent and a decimal.
If I said, we have used up 50% of our storage space, we all have a clear picture. But, if we wanted to do any mathematical computation then we have to convert it to a useful number, which means we have to convert it to its decimal form of 0.5.
So how do we fix the problem?
Radians! If we convert degrees into radian measure, then we are allowed to treat trigonometric functions as functions with domains of real numbers rather than angles!
What is a radian?
Okay, so radian is an angle with vertex at the center of a circle that intercepts an arc on the circle equal in length to the radius of the circle. Or as summarized by Teacher’s Choice, one radian is the angle of an arc created by wrapping the radius of a circle around its circumference.Huh?
Picture a circle.
Now we know two things:
- A circle has 360 degrees all the way around.
- The circumference of any circle is just the distance around it. This means that the number of radii in the circumference is 2pi.

Formula for the Circumference of a Circle
Here’s another way to look at it…
Remember when we created our unit circle? Well, we specified that our radius was the value of 1, right? So, if we then want to calculate our circumference of this unit circle, our distance around would be 2pi.
Ah, now I see. So in our unit circle, we have a circumference of 2pi, which means I’ve gone all the way around which is just like rotating 360 degrees as seen in the unit circle diagram below.

Unit Circle Diagram
Degrees to Radians Formula
Well, now that we know that 360 degrees (rotational measure) equals 2pi radians (distance measure), we can switch back and forth quickly and easily. In fact, we make it even nicer by simplifying and using the conversion: 180 degrees = pi radians!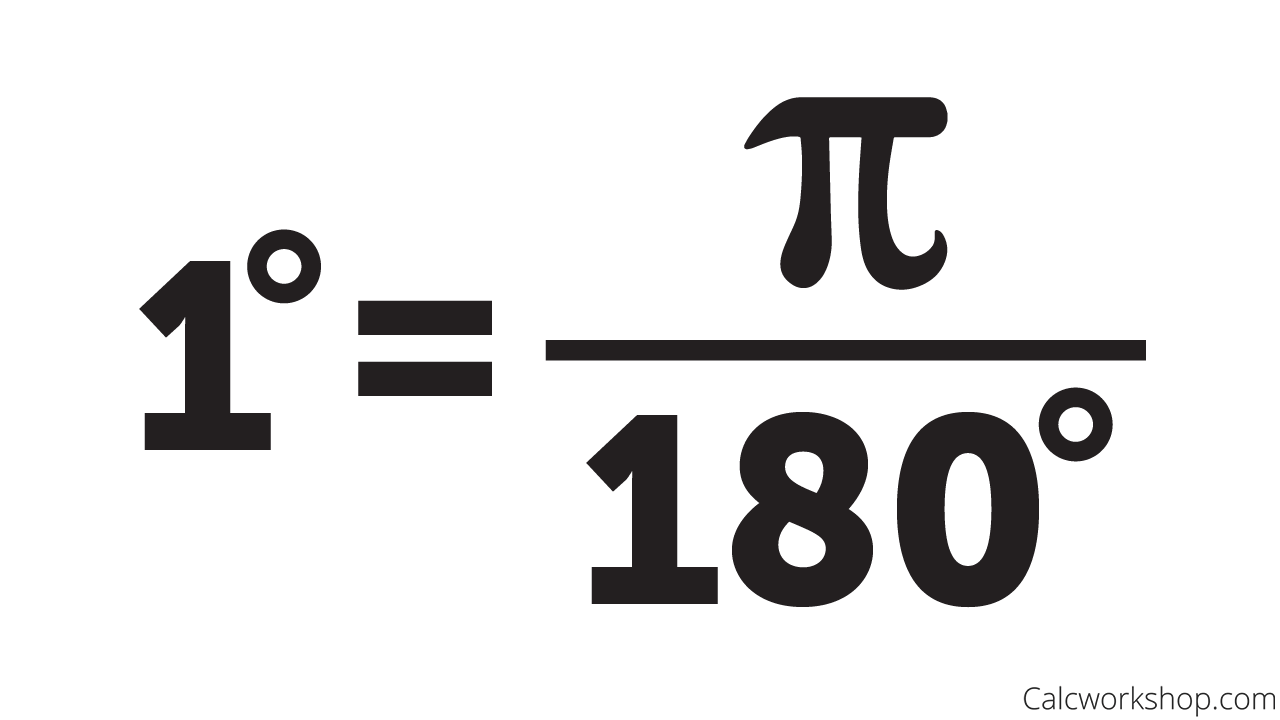
Degrees to Radians Formula
In more advanced mathematics, the use of radian measure is preferred and often required to solve problems. To deal limits and derivatives, which helps us to explain how things change over time, we have to use radians – and over time, you will see that radians are easy, fun, and very, very helpful!
Trust me…
…radians are friends!
Converting Radians to Degrees
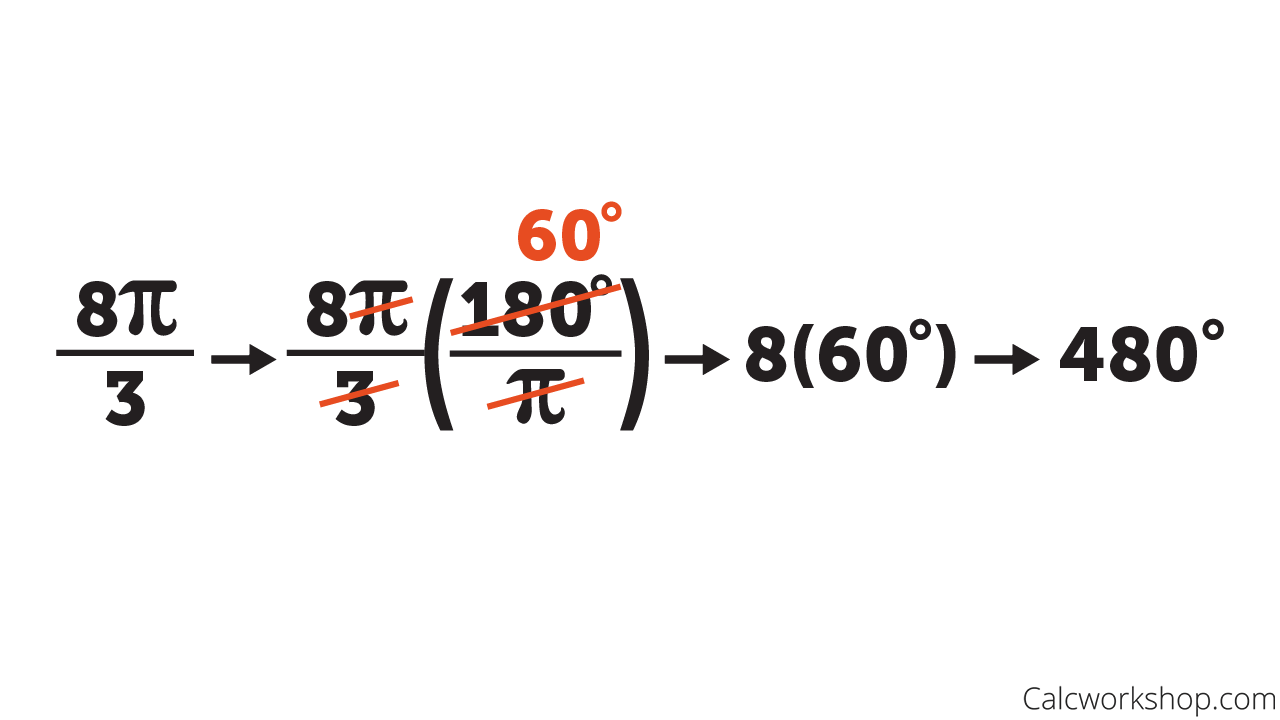
Converting 8pi/3 to Degrees
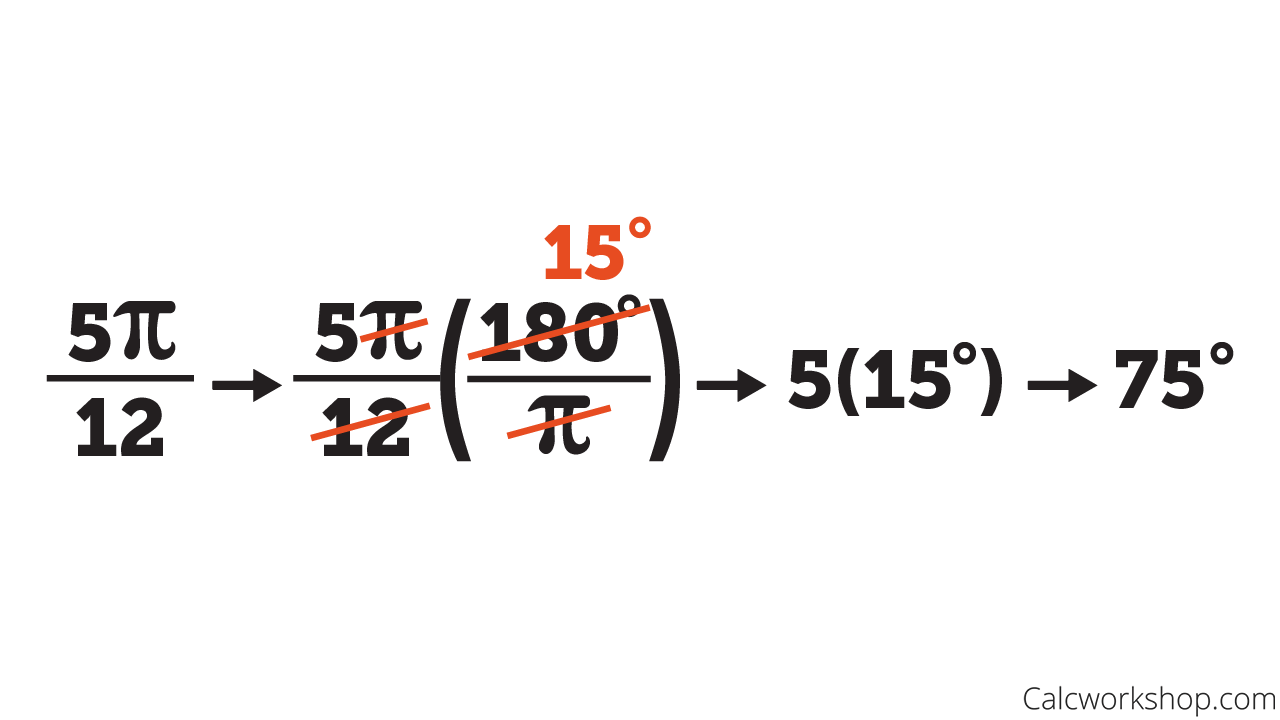
Converting 5pi/12 to Degrees
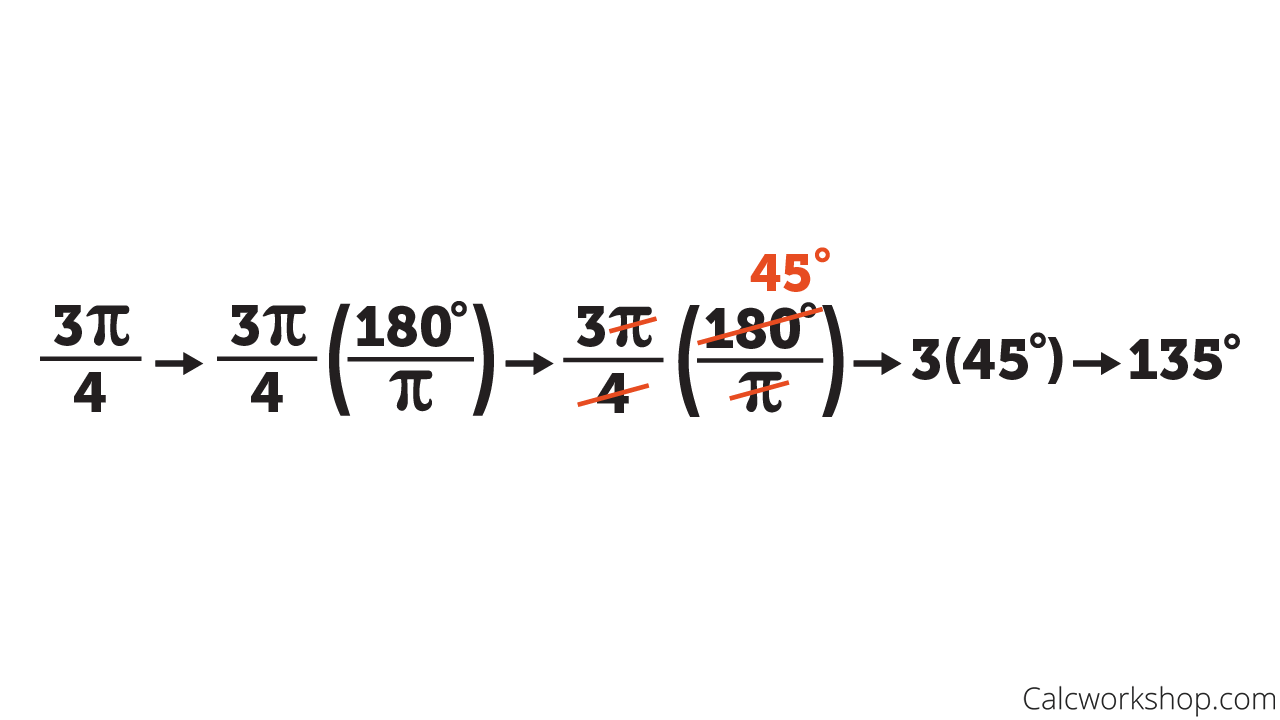
Converting 3pi/4 to Degrees
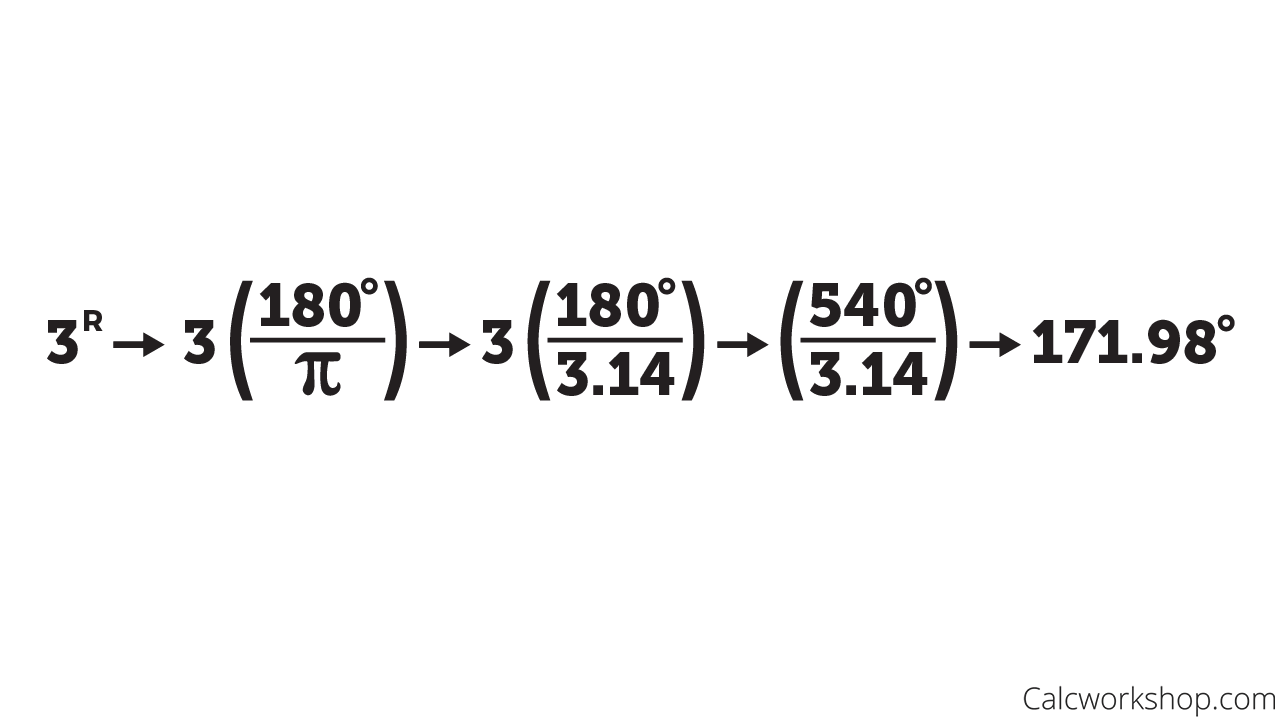
Converting 3 Radians to Degrees
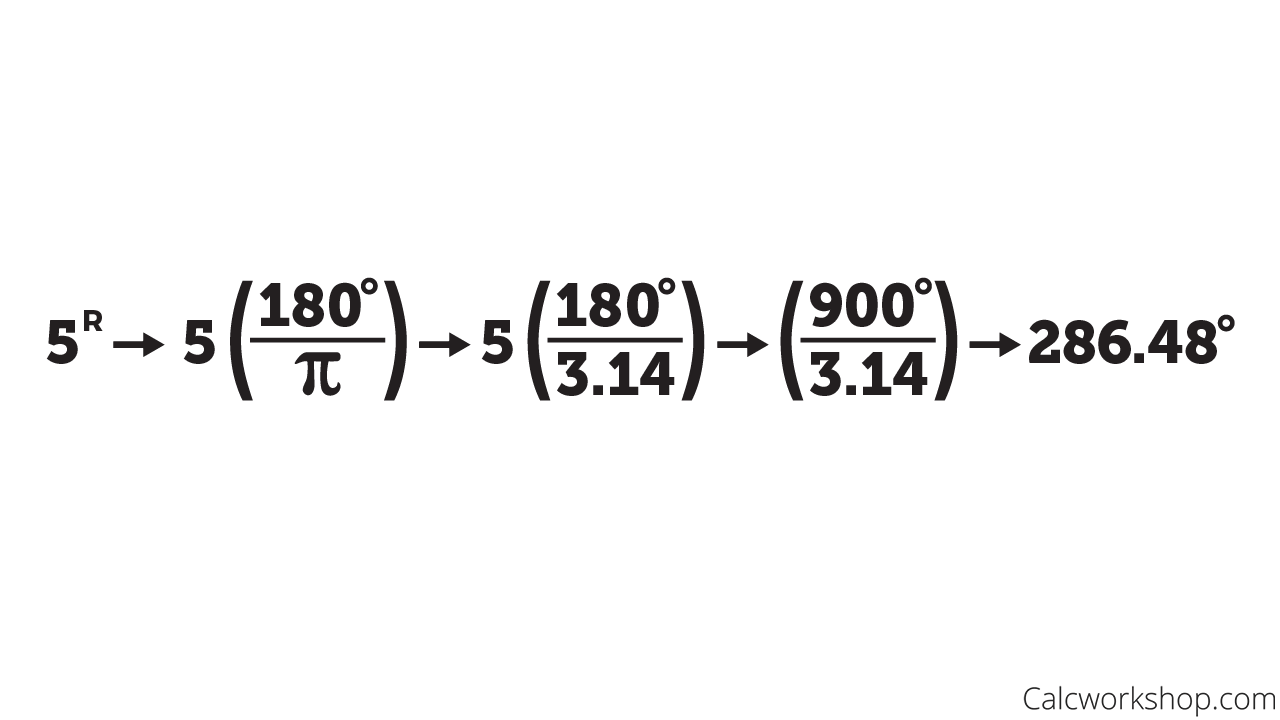
Converting 5 Radians to Degrees
Changing Degrees to Radian
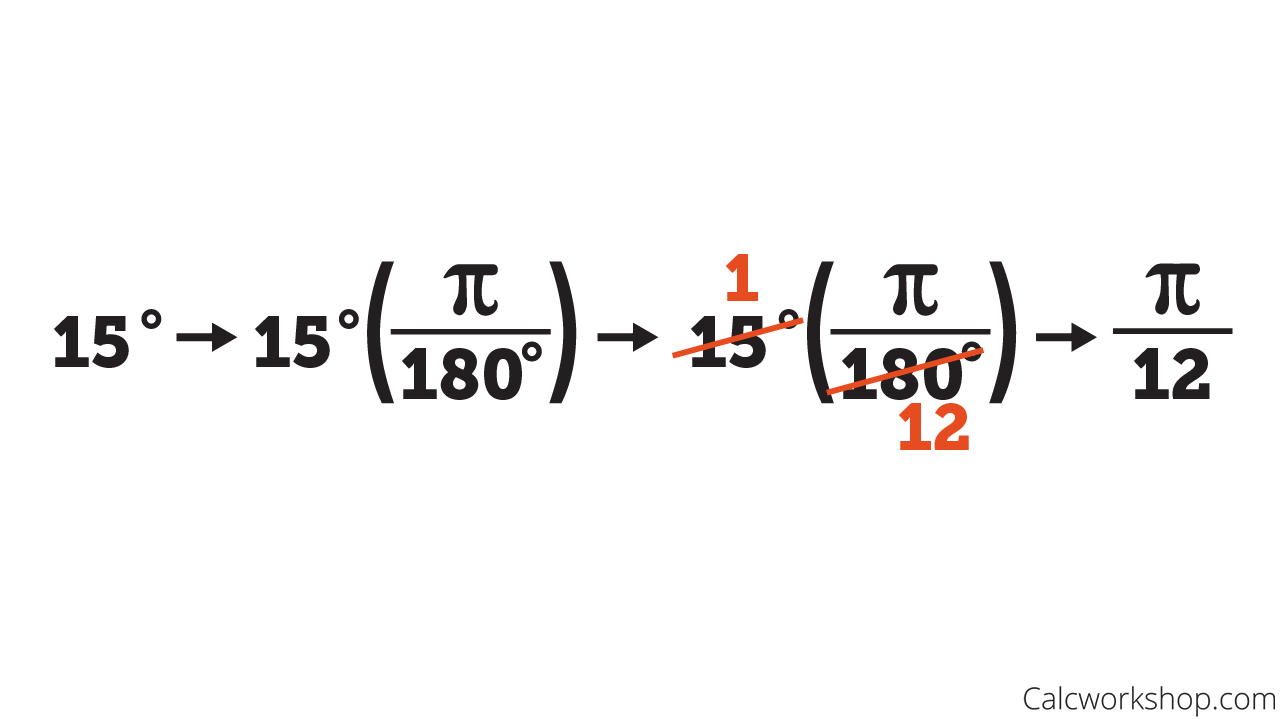
Converting 15 Degrees to Radians

Converting 45 Degrees to Radians
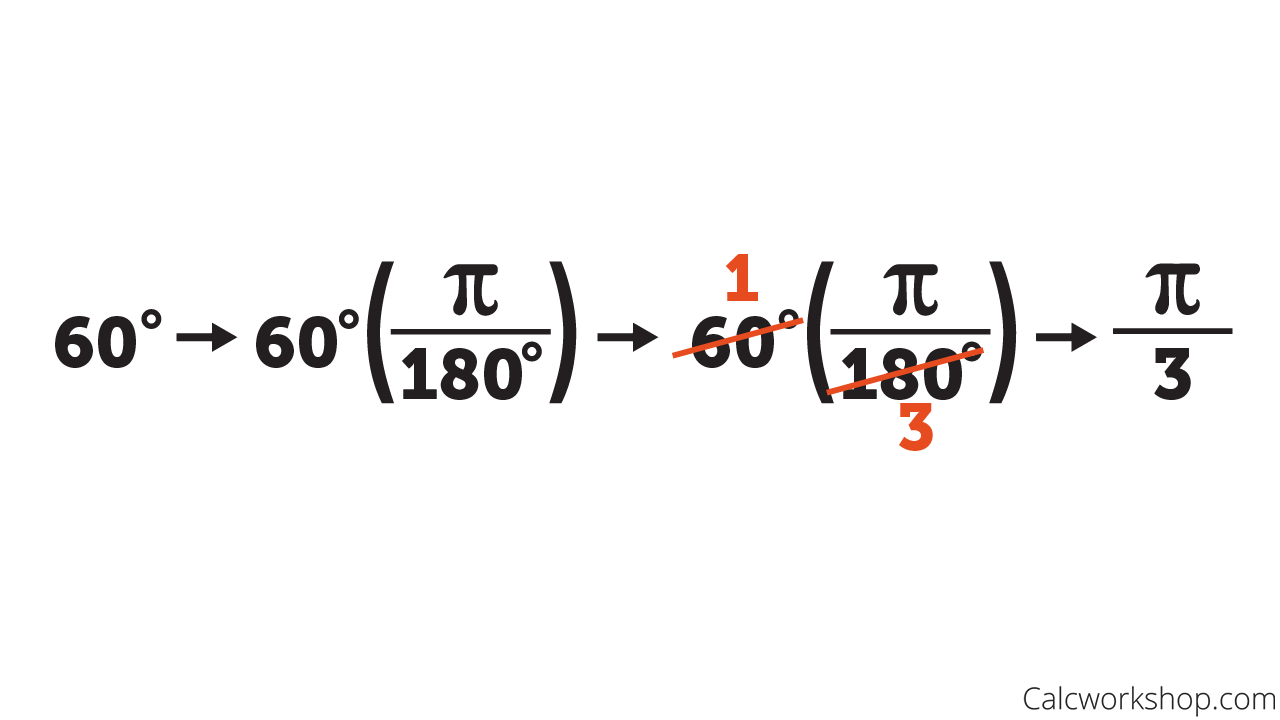
Converting 60 Degrees to Radians
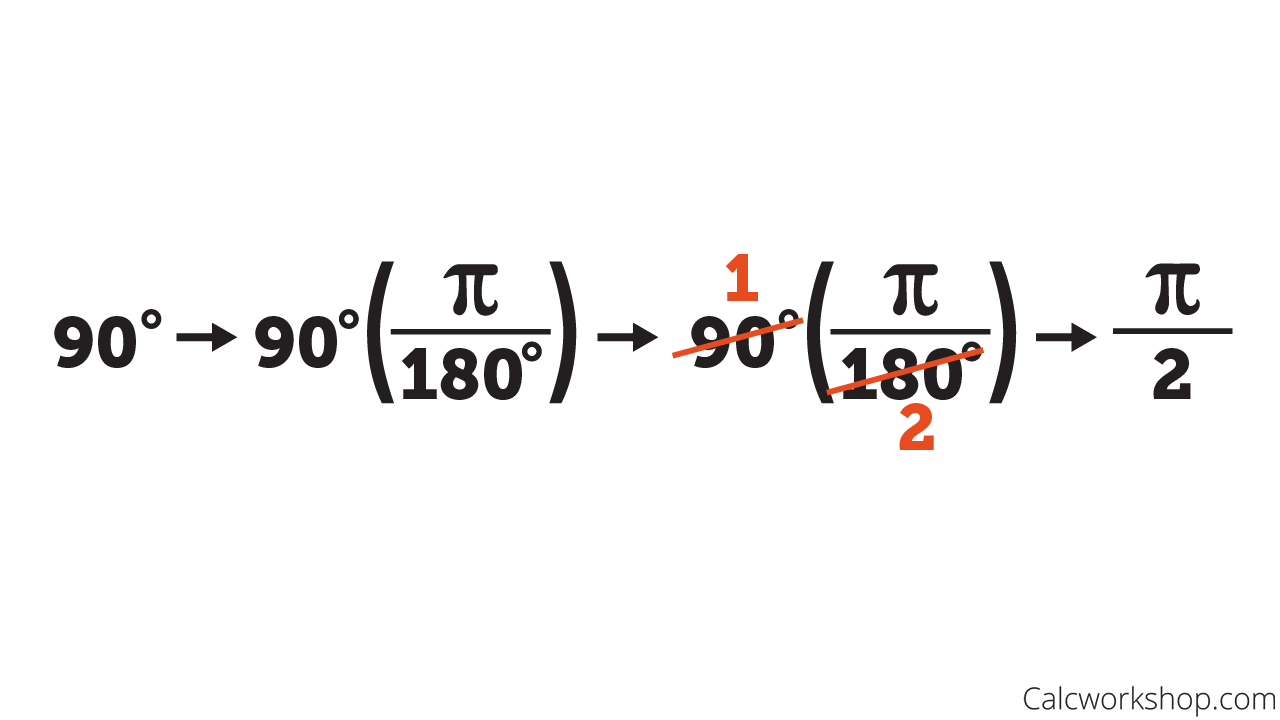
Converting 90 Degrees to Radians
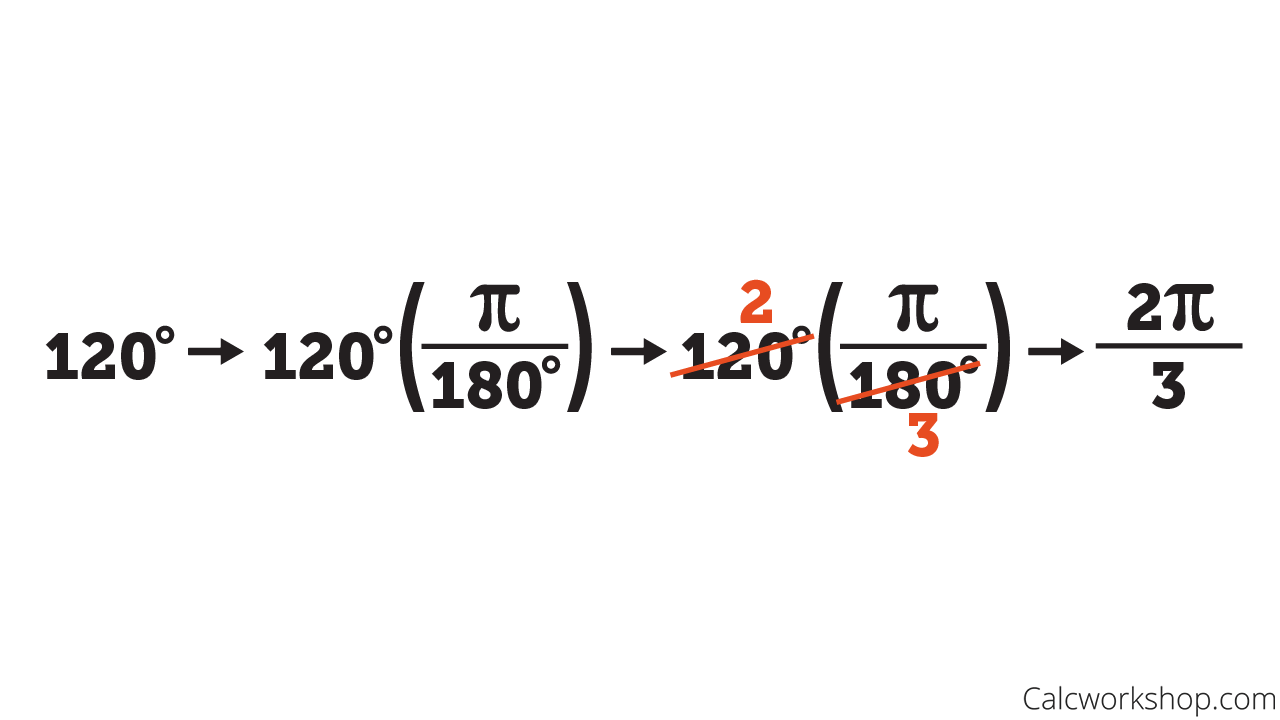
Converting 120 Degrees to Radians
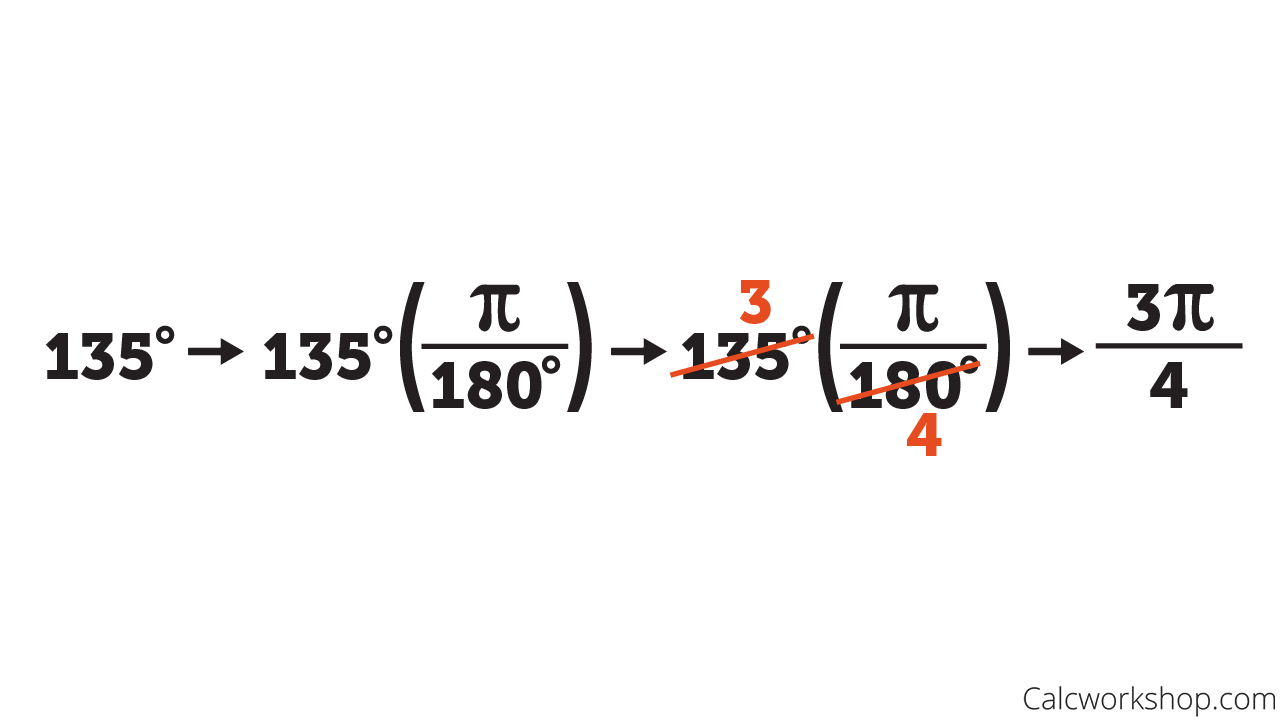
Converting 135 Degrees to Radians
So in this lesson, we’re going to learn all about how to converts from degrees to radians and from radians to degrees.
Radians & Degrees Conversion Handout
- Converting Degrees and Radians: See how the conversion between radians and degrees is performed. This handout includes 21 worked examples.
Converting Radians to Degrees Video
Monthly, Half-Yearly, and Yearly Plans Available
Get My Subscription Now
Not yet ready to subscribe? Take Calcworkshop for a spin with our FREE limits course







0 Comments